Statistiques concernant les contrats de tournois de bridge de haut niveau
Auteur : Robert Mahl
Email : mahl [at] cri . ensmp . fr
Résumé :
Nous utilisons des méthodes statistiques pour étudier les contrats obtenus par des joueurs de haut niveau au jeu de bridge. Les contrats déclarés par les humains et leurs résultats sont comparés à leurs homologues du double mort. L'étude se place dans le cadre des duplicates scorés en IMPs, et ne concerne pas les tournois par paires.
Introduction
Nous étudions statistiquement le niveau et la réussite des contrats obtenus par des joueurs dans des compétitions internationales.
Nous exploitons une base de données de donnes de bridge effectivement jouées en duplicate dans des compétitions de niveau mondial, avec une notation en IMPs, dans la période 1990-2016. Cette base comporte 128.171 donnes, dont 116.102 donnes avec une information complète sur le déroulement (enchères, jeu de la carte)
Tableau 1:
Nature des contrats déclarés par les joueurs
NiveauMineureMajeureSA| Total (et % de la colonne)
| | Partielle | 12252 (28,9%)21155 (49,8%)9054 (21,3%)42461 (36,6%)
| Manche | 5926 ( 9,1%)35859 (55,1%)23276 (35,8%)72200 (56,0%)
| Petit chelem | 2847 (38,0%)3938(52,5%)716 ( 9,5%)7501 ( 6,5%)
| Grand chelem | 391 (36,2%)552 (51,2%)136 (12,6%)1079 ( 0,9%)
Total21416 (18,4%)61504 (53,0%)33182 (28,6%)| 116102 ( 100%)
| | | | | | | | | | | | | | | | | | | | | | | | | |
Ce tableau montre que les majeures sont préférées aux mineures dans tous les contrats, mais particulièrement dans les manches. D'autre part, les contrats à Sans Atout sont nettement plus nombreux dans les manches que dans les partielles ou dans les chelems.
Tableau 2 :
Pourcentage de contrats contrés punitifs par niveau et atout
NiveauMineureMajeureSA
Non contréContré
Non contréContré
Non contréContré
| Partielle
| 91,1%
8,9%
95,1%
4,9%
97,2%
2,8%
| Manche
| 72,6%
27,4%
90,4%
9,6%
98,5%
1,5%
| Petit chelem
| 92,0%
8,0%
91,4%
8,6%
97,7%
2,2%
| Grand chelem
| 76,2%
23,8%
90,9%
9,1%
92,6%
| 7,4%
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
Les contrats à Sans Atout sont rarement contrés. Les manches en mineure le sont beaucoup plus souvent, de même que les grands chelems en mineures, probablement car ces contrats sont soupçonnés d'être des défenses qui chutent. Les partielles en majeures ne sont que rarement contrées, puisque la pénalité en cas de succès du contrat devient très importante.
Au total, il y a 8534 contrats contrés punitif (7,4 %), et seulement 120 contrats surcontrés (0,1 %).
L'annonce "contre" (informatif ou punitif) apparaît dans 32,2% des séquences d'enchères. Le "contre" purement informatif, c'est-à-dire non final dans les enchères et donc non punitif, apparaît dans 28,2 % des séquences d'enchères.
| Niveau | Séquences d'enchères ayant comporté
au moins un contre non punitif
|
| Partielle
| 33 %
| Manche
| 25,8 %
| Petit chelem
| 23,5 %
| Grand chelem
| 22,2 %
| Moyenne générale
| 28,2 %
| | | | |
S'il est peu surprenant de trouver des contres informatifs au niveau des partielles, il peut sembler surprenant d'en trouver un aussi grand nombre au niveau des chelems, ce qui témoigne du caractère compétitif des enchères modernes.
Sur les 116102 contrats, 74651 (64,3%) ont gagné.
Taux de succès des contrats
NiveauMineureMajeureSA
Non contréContré
Non contréContré
Non contréContré
| Partielle
| 61,5%
20,3%
64,3%
16,1%
65,6%
34,0%
| Manche
| 62,1%
20,2%
70,6%
23,0%
70,6%
35,2%
| Petit chelem
| 68,5%
20,6%
70,7%
13,6%
71,4%
31,2%
| Grand chelem
| 67,8%
4,3%
74,5%
10,0%
77,8%
| 10,0%
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
Ce tableau montre queles grands chelems ne sont contrés que lorsqu'ils ont une très sérieuse probabilité de chuter. A l'inverse, plus de 34 % des contrats contrés à Sans Atout gagnent, ce qui explique vraisemblablement le faible taux de Contre des enchères à SA.
Bien que les 120 surcontres de notre base soient anecdotiques, et que quelques-uns correspondent à des mésententes entre partenaires (par exemple un surcontre SOS étant interprété à tort par le partenaire comme une main forte), il est intéressant de noter les taux de réussite de ces contrats et leur répartition :
Répartition des contrats surcontrés
NiveauMineureMajeureSA
| Partielle | 26 | 16 11 | 2 10 | 4
| Manche | 18 | 7 29 | 1019 | 11
| Petit chelem | 3 | 1 3 | 20
| Grand chelem | 0 1 | 1| 0
| | | | | | | | | | | | | | | | |
Dans chaque case de ce tableau, on trouve le nombre de contrats surcontrés et le nombre de contrats réussis. Comme on le voit, le surcontre a eu dans l'ensemble un succès mitigé.
Le seul cas de grand chelem surcontré (et réussi) est suffisamment curieux pour être donné ici à titre d'illustration :
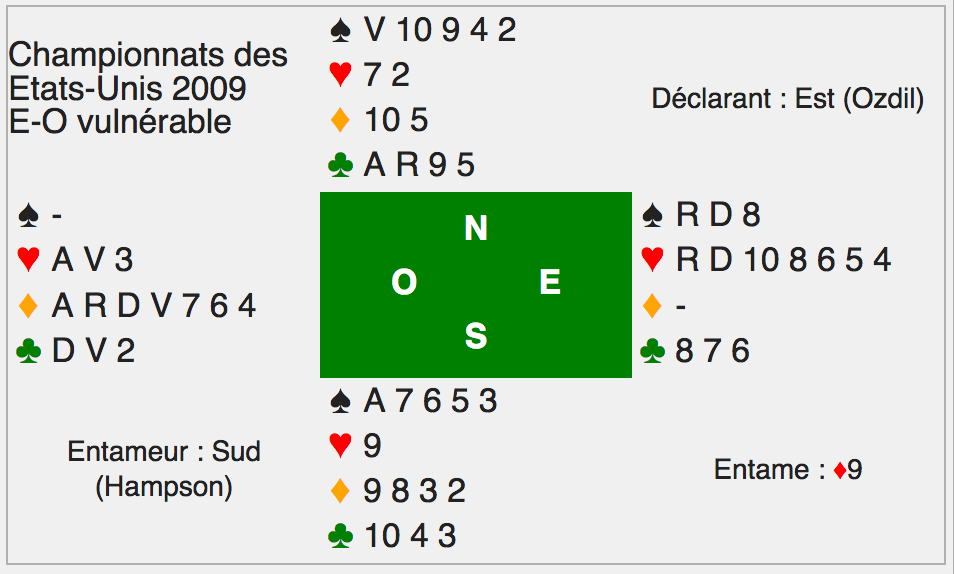
|
Les enchères "à la hussarde" :
Sud
Ouest
Nord
Est
Passe
2♣
Passe
2♥
Passe
3♦
Passe
3♥
Passe
6♥
Passe
7♥
Passe
Passe
Contre
Surcontre !
| Tous passent
| | | | | | | | | | | | | | | | | | | | |
L'entame malheureuse à Carreau donne évidemment toutes les levées au déclarant. Dans l'autre salle, Nord jouait 6♠X et chutait de 5 levées pour 1100 points.
| |
Le double mort est une variante du bridge dans laquelle les 2 camps (NS et EO) jouent l'un contre l'autre de façon optimale, en pleine connaissance des 4 mains du jeu. C'est une méthode utilisée dans tous les logiciels de jeu de haut niveau pour évaluer statistiquement le déroulement d'une donne, ses résultats, et les meilleurs contrats.
Détermination du PAR en double mort
Le PAR ou contrat de PAR correspond au niveau optimal des enchères du bridge, déterminé classiquement en double-mort comme suit : on examine les contrats optimaux des 2 camps (Nord-Sud et Est-Ouest) tandis que chaque camp connaît les 4 mains. Chaque camp enchérit à tour de rôle, s'il y a une enchère meilleure pour lui que la dernière faite par l'autre camp. Le processus s'arrête lorsqu'il n'y a pas de meilleure enchère, et on a ainsi atteint l'équilibre de Nash.
Le PAR est donc :
- soit le contrat optimal de l'un des camps,
- soit un contrat plus élevé qu'aucun des 2 camps ne peut améliorer, et dont le score est compris en valeur algébrique entre les scores des contrats optimaux des deux camps. D'où la qualification de contrat sous-optimal. Un contrat sous-optimal est donc typiquement un contrat de défense.
Exemple : considérons la donne suivante
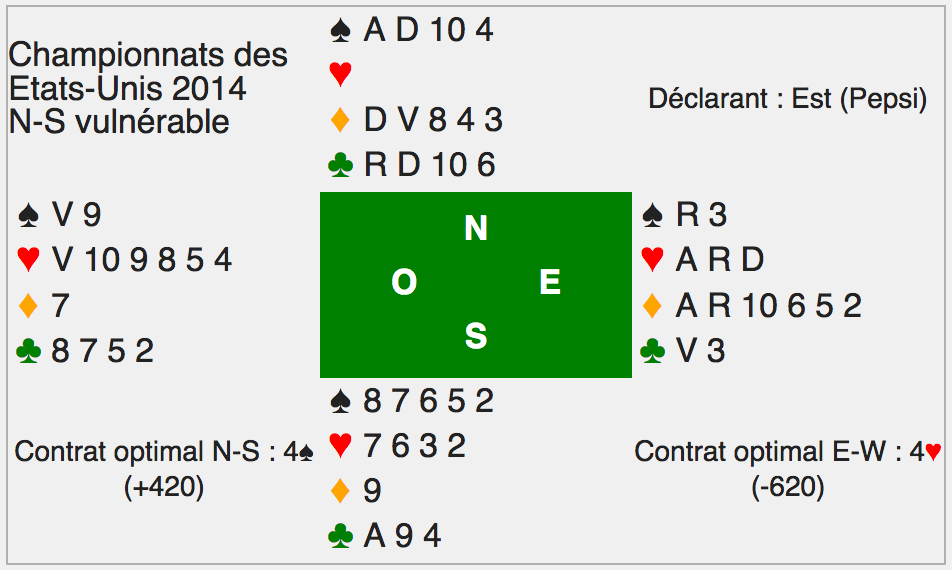
Les gains de Nord-Sud sont comptés positivement, ceux de Est-Ouest sont comptés négativement.
- Le camp Est-Ouest est arrivé à l'enchère, optimale pour son camp, de 4♥. Si ce contrat était accepté, le gain, compté négativement puisqu'il s'agit de Est-Ouest, serait de -680.
- Le camp Nord-Sud déclare son contrat optimal de 4♠. Si ce contrat était accepté, le gain pour son camp serait de +420.
- Est-Ouest annonce alors 5♥. Ce contrat chute de 1, le score est donc de +200 pour Nord-Sud. Ce score est bien compris dans l'intervalle [-680, +420] et est donc parfaitement acceptable. Plus personne ne surenchérit.
Comparaison entre les résultats des experts humains et double mort
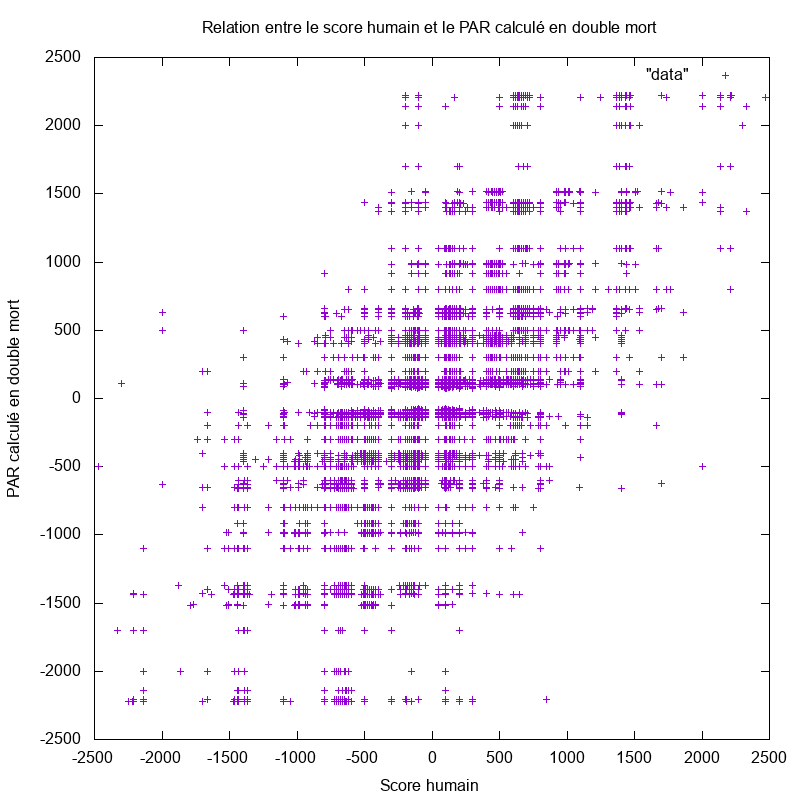
La figure 1 montre la relation entre le score obtenu par les experts internationaux (en abcisse) et la valeur du PAR, calculée en double mort (en ordonnée). Sur chacun des axes, le score est compté positivement si Nord-Sud marque dans sa colonne, et négativement si c'est Est-Ouest qui gagne les points.
| Nombre de levées double mort
| Contrats à une couleur
| Contrats à SA
| | Nombre de contrats à la couleur
| Nombre moyen de levées à la couleur
(variance)
| Nombre de contrats à SA
| Nombre moyen de levées à SA
(variance)
| 6 | 2698 | 6.44 (0.76)
| 2585 | 6.61 (1.44)
| | 7 | 6372 | 7.33 (0.68)
| 4637 | 7.42 (1.24)
| | 8 | 12413 | 8.17 (0.62)
| 6941 | 8.23 (1.25)
| | 9 | 17628 | 9.06 (0.54)
| 6895 | 9.13 (1.08)
| | 10 | 18400 | 9.95 (0.51)
| 5273 | 9.91 (1.07)
| | 11 | 14053 | 10.87 (0.46)
| 3149 | 10.69 (1.07)
| | 12 | 7755 | 11.79 (0.40)
| 1584 | 11.56 (0.94)
| | 13 | 2226 | 12.62 (0.36)
| 423 | 12.38 (1.24)
| |
| |
Figure 1 : Relation entre le score des joueurs humains et le PAR calculé en double mort.
A gauche, représentation par des points de la correspondance entre les scores humains et double-mort.
A droite, correspondance entre le nombre de levées réalisé en double mort et le nombre de levées réalisé par les joueurs humains ; en italiques, la variance exprimée en nombre de levées, beaucoup plus importante pour les contrats à Sans Atout, à la fois à cause de l'incertitude créée par l'entame que celle du reste du jeu à la carte.
La relative linéarité de la correspondance entre le score des joueurs et le PAR calculé en double mort nous suggère d'utiliser la technique du double mort pour étudier le comportement des joueurs humains.
Le tableau suivant compare, pour les mêmes donnes, les contrats de PAR obtenus en double mort et ceux des humains, par niveau de contrat.
Correspondance entre niveau des contrats humains et double-mort
Niveau contrats humainsNiveau contrats double-mort
Partielles
Manches
Petits chelems
Grands chelems
Partielles
31217 (73,5%)
10762 (25,3%)
414 (1,0%)
68 (0,2%)
Manches
14603 (22,4%)
41026 (63,1%)
7697 (11,8%)
1735 (2,7%)
Petits chelems
58 (0,1%)
1712 (22,8%)
3879 (51,7%)
1852 (24,7%)
Grands chelems
2 (0,2%)
44 (4,1%)
194 (18,0%)
| 839 (77,8%)
| | | | | | | | | | | | | | | | | | | | | | | | | | |
Dans l'ensemble, la correspondance est bonne, toutefois :
- le double mort est plus pessimiste pour les manches
- le double mort est plus optimiste pour les chelems.
La cause de ces distorsions est différente dans les 2 cas :
- Concernant les manches, c'est lié au fait double-mort imagine une entame optimale de son adversaire, alors qu'en pratique le joueur humain a une probabilité de 27 % de faire une entame malheureuse à SA et de 16 % à un contrat à la couleur. A ce sujet, voir: Statistiques sur les entames .
- Concernant les chelems, c'est dû au fait que le double mort a un réel avantage par rapport à l'humain pour lire les impasses et les fins de coup. Par exemple, un humain ne déclarera pas un grand chelem qui se fait sur une impasse, alors que le double mort sait tout sur les distributions adverses.
Nous distinguons 3 types de séquences d'enchères ;
- Le camp du déclarant a enchéri sans aucune intervention adverse
- Les adversaires ont contré au moins une fois une annonce du camp déclarant avant l'annonce du contrat final, mais n'ont annoncé eux-même aucun contrat
- Les adversaires ont annoncé eux-même un ou plusieurs contrats avant l'annonce du contrat final.
Dans chaque type, le contrat final peut être contré ... ou pas.
La fréquence des différents cas de figure est donnée dans le tableau suivant, ainsi que le taux de réussite des contrats.
Nature des enchèresNombre de casTaux de succès des contratsTaux de contrats
contrés punitif
Non compétitives
46,5 %
70,6 %
1,6 %
Contre informatif
mais sans annonce
4,5 %
64,8 %
9,8 %
Compétitives
49,0 %
58,2 %
| 12,6 %
| | | | | | | | | | | | | | | |
Sans surprise, on voit que les contrats déclarés dans un total silence adverse sont plus souvent réussis par les déclarants. Les séquences d'enchères ayant subi des contres informatifs (généralement d'appel) ont des taux de réussite inférieurs. Enfin, lorsque les enchères sont vraiment compétitives, le taux de réussite est encore réduit du fait que beaucoup de contrats sont déclarés en défense, avec une très forte probabilité de chute.
Egalement sans surprise, nous apprenons que seulement 1,6 % des contrats déclarés librement sont contrés.
Comparaison du jeu de la carte humain / double mort selon la compétitivité
Nature des enchèresSurcroît de succès humain
par rapport au double mort
(en % de contrats réussis)
Surcroît de levées humain
par rapport au double mort
Non compétitives
0,1 %
-0,004
Contre informatif
mais sans annonce
1,3 %
0,018
Compétitives
2,1 %
| 0,049
| | | | | | | | | | | | |
Le tableau ci-contre ne concerne que les contrats à la couleur. Il montre que les contrats humains ont quasiment le même succès que le double mort dans les enchères non compétitives, mais que le déclarant humain performe mieux au jeu de la carte dans les compétitives. On peut en inférer que les nombreuses indications apportées par les enchères compétitives profitent davantage au jeu de la carte du déclarant qu'au jeu de la carte du flanc.
Les tableaux qui suivent sont l'équivalent du tableau 1 pour les 3 types de séquences déclaratives :
Sans intervention adverse:
Nature des contrats déclarés par les joueurs
NiveauMineureMajeureSA| Total (et % de la colonne)
| | Partielle | 3201 (18,0 %)
8172 (46,1 %)
6366 (35,9 %)
17739 (32,9 %)
| Manche
| 1336 ( 4,2 %)
15928 (50,4 %)
14313 (45,3 %)
31577 (58,5 %)
| Petit chelem | 1429 (35,1 %)
2101 (51,6 %)
542 (13,3 %)
4072 ( 7,5 %)
| Grand chelem
| 197 (32,7 %)
307 (51,0 %)
98 (16,3 %)
602 ( 1,1 %)
Total6163 (11,4 %)
26508 (49,1 %)
21319 (39,5 %)
| 53990
| | | | | | | | | | | | | | | | | | | | | | | | | |
Sans intervention adverse, les contrats à SA sont plus nombreux dans les différents compartiments d'enchères.
Avec contre(s) informatif(s) sans annonce des adversaires :
Nature des contrats déclarés par les joueurs
NiveauMineureMajeureSA| Total (et % de la colonne)
| | Partielle | 667 (34,1 %)
1077 (55,1 %)
211 (10,8 %)
1955 (37,7 %)
| Manche
| 254 ( 9,6 %)
1773 (67,2 %)
610 (23,1 %)
2637 (50,9 %)
| Petit chelem | 177 (35,7 %)
288 (58,1 %)
31 ( 6,2 %)
496 ( 9,6 %)
| Grand chelem
| 24 (26,1 %)
52 (56,5 %)
16 (17,4 %)
92 ( 1,8 %)
Total1122 (21,7 %)
3190 (61,6 %)
868 (16,8 %)
| 5180
| | | | | | | | | | | | | | | | | | | | | | | | | |
Dès lors qu'il y a un contre informatif des adversaires, le taux de contrats à SA s'effondre, sauf pour les grands chelems. C'est aussi la catégorie d'enchères où les contrats dans les majeures sont les plus nombreux, quel que soit le niveau de ces contrats. On peut supposer que le type des mains de la donne se prête mieux à un contrat en majeure, mais aussi que les déclarants privilégient la majeure lorsqu'ils sentent une menace du côté des adversaires.
Avec annonces adverses :
Nature des contrats déclarés par les joueurs
NiveauMineureMajeureSA| Total (et % de la colonne)
| | Partielle | 8384 (36,8 %)
11906 (52,3 %)
2477 (10,9 %)
22767 (40,0 %)
| Manche
| 4336 (14,1 %)
18158 (58,9 %)
8353 (27,1 %)
30847 (54,2 %)
| Petit chelem | 1241 (42,3 %)
1549 (52,8 %)
143 ( 4,9 %)
2933 ( 5,2 %)
| Grand chelem
| 170 (44,2 %)
193 (50,1 %)
22 ( 5,7 %)
385 ( 0,7 %)
Total14131 (24,8 %)
31806 (55,9 %)
10995 (19,3 %)
| 56932
| | | | | | | | | | | | | | | | | | | | | | | | | |
Avec intervention adverse, les contrats dans les mineures prennent de l'essor, au détriment des contrats dans les majeures et à SA.
Répartition des contractants selon la vulnérabilité des 2 camps
Lorsque les 2 camps sont vulnérables ou lorsque aucun des deux n'est vulnérable, le nombre de contrats est évidemment statistiquement le même dans les 2 camps. Tel n'est pas le cas lorsque l'un des camps est vulnérable et l'autre ne l'est pas :
Répartition des contrats selon la vulnérabilité
du camp contractant et du camp adverse
VulnérabilitéContrats déclarés en championnatsContrats déclarés en double mort
Camp ContractantCamp défense
Non vulnérable
Vulnérable
27,8 %
32,7 %
Vulnérable
Non vulnérable
22,1 %
17,2 %
Total
50%
| 50%
| | | | | | | | | | | | | | | | |
Dans ce tableau, les pourcentages sont donnés par rapport au nombre total de contrats joués. Etant donné que les contrats où l'un des camps est vulnérable et l'autre pas représentent la moitié du nombre total de contrats, il est normal que la somme des colonnes fasse 50 %.
On devait s'attendre à ce qu'en situation non vulnérable contre vulnérable, les contrats soient plus nombreux dans le camp des non-vulnérables (souvent en attaque). La surprise vient du fait que le phénomène est plus accentué en double-mort. L'explication est que les joueurs humains, même champions, n'ont souvent pas les moyens de se rendre compte qu'une défense serait lucrative. Ce tableau montre que dans (32,7 % - 25 %) = 7,7 % de l'ensemble des donnes, le double-mort en position favorable de vulnérabilité défend contre son adversaire, et si on ramène ce pourcentage aux 25 % de cas où l'on est NV contre V, cela montre plus de 30 % de défenses NV contre V, alors que le ratio correspondant de l'expert humain est de (27,8 % - 25 %) / 25 % = 11,2 % beaucoup plus faible.
Proportion d'enchères sous-optimales en double mort
En double-mort, dans 81,6 % des cas le contrat optimal de l'un des 2 camps est aussi le contrat de PAR. Dans les 18,4 % des cas restants, les joueurs arrivent à un compromis plus élevé comme celui de l'exemple ci-dessus.
Contrats optimaux et contrats sous-optimaux déclarés et joués en double-mort : répartition et succès
NiveauRépartition des contrats% de succès des contrats
OptimauxSous-optimaux
OptimauxSous-optimaux
| Partielle
| 37879 (82,6 %)
8001 (17,4 %)
100 %
4,6 %
| Manche
| 43910 (82,0 %)
9634 (18,0 %)
100 %
1,9 %
| Petit chelem
| 10071 (82,7 %)
2113 (17,3 %)
100 %
0 %
| Grand chelem
| 2905 (64,6 %)
1589 (35,4 %)
100 %
| 0 %
| | | | | | | | | | | | | | | | | | | | | | | |
Le pourcentage de contrats optimaux qui sont au PAR est remarquablement constant selon le niveau des contrats, à l'exception des grands chelems. On se souvient d'ailleurs que c'est à cause d'une défense (réussie) par la déclaration d'un grand chelem par l'équipe Meckstroth-Rodwell que les règles internationales du bridge furent modifiées en 1986 par un alourdissement des pénalités pour les levées de chute non-vulnérable. Certes, nos statistiques sont calculées selon les nouvelles règles, mais elles ne suffisent pas pour dissuader les grands chelems en défense, du moins en double-mort.
D'autre part, les chances de succès des contrats sous-optimaux en double mort sont faibles, et nulles au niveau des chelems. Les contrats sous-optimaux qui réussissent en double mort sont obligatoirement réalisés dans une autre couleur que la couleur optimale : en effet, si c'étaient des contrats supérieurs qui réussissaient dans la même couleur, ils seraient qualifiés de contrats forcés (cf infra).
La typologie des contrats sous-optimaux en double mort montre, sans surprise, la rareté des contrats à SA, mais aussi que la proportion de ces contrats défensifs entre mineures et majeures n'est pas du tout la même selon les différents niveaux de contrats :
Contrats sous-optimaux en double mort
NiveauMineureMajeureSA
| Partielle
| 4199 (52,5 %)
3187 (39,8 %)
615 (7,7 %)
| Manche
| 3222 (33,4 %)
5724 (59,4 %)
688 (7,1 %)
| Petit chelem
| 840 (39,8 %)
1255 (59,4 %)
18 (0,9 %)
| Grand chelem
| 883 (55,6 %)
706 (44,4 %)
| 0 ( 0 %)
| | | | | | | | | | | | | | | | |
Lorsque le niveau du contrat de PAR dépasse le niveau minimum que le contractant aurait souhaité atteindre, sans pour autant le mener à un niveau qui chute, le score du contractant est le même que s'il avait joué le contrat inférieur. Par exemple, le score de 4♠+1 est le même que celui de 5♠=, mais le déclarant a été forcé de monter à 5♠ car sinon les adversaires auraient joué un contrat plus avantageux pour eux. Les contrats forcés sont ainsi des contrats optimaux et réussis aux niveaux de 2, 3, 5 à une majeure, 2, 3, 4 à une mineure, et 2, 4 ou 5 à SA. Alors que le forçage à la couleur est très fréquent dans les partielles, il l'est nettement moins dans les manches et est inexistant dans les chelems.
Répartition des Contrats optimaux en double mort entre contrats non forcés et forcés
NiveauNon forcéForcé
| Partielle
| 12784
25095
| Manche
| 41016
| 2894
| | | | | | | |
Mais tout ceci est un peu théorique puisque calculé en double mort. Voyons ce qu'il en est pour les vrais joueurs des championnats internationaux.
Les contrats sous-optimaux sont faciles à définir et à détecter pour le double mort, mais moins faciles pour les contrats joués par les humains. Aussi, nous introduisons une nouvelle classification basée sur un critère objectif et toujours mesurable automatiquement.
Nous qualifierons dans ce qui suit de contrat légitime tout contrat joué par le camp dont le contrat optimal (calculé en double mort) permet d'atteindre le niveau d'enchères le plus élevé. Par opposition, les contrats non légitimes sont qualifiés de contrats de défense. Nous parlerons de même de camp légitime et de camp de défense.
Par exemple, supposons que N-S a un contrat optimal de 3SA= (juste fait), et que E-O a un contrat optimal de 1♣+3 (avec 3 surlevées). Le contrat de 4♣ est alors considéré comme légitime, puisqu'il est déclaré dans la même couleur que le contrat optimal de 1♣ et que tout contrat de N-S supérieur à 4♣ devrait chuter en double mort. Le camp E-O est légitime, même s'il déclare un contrat différent de 4♣ (et même s'il chute), et le camp N-S est en défense quel que soit son contrat final, même si son contrat est inférieur à son contrat optimal et même s'il est supérieur au PAR et réussit quand même.
Nous trouvons alors la répartition suivante entre déclarants légitimes et de défense :
Répartition des contractants entre légitimes et de défense
LégitimitéJoueurs humainsDouble mort
| Camp défense
| 22338 (19,2 %)
20728 (17,9 %)
| Camp légitime
| 93764 (80,8 %)
| 95374 (82,1 %)
| | | | | | | |
Répartition des contractants légitimes et en défense, selon le type de contrat
Niveau de contratJoueurs humainsDouble mort
Camp défense
Camp légitime
Camp défense
Camp légitime
Partielle
15366 (36.2 %)
27095 (63.8 %)
7714 (16.8 %)
38166 (83.2 %)
Manche
6567 (10.1 %)
58494 (89.9 %)
9318 (17.4 %)
44226 (82.6 %)
Petit chelem
325 ( 4.3 %)
7176 (95.7 %)
2107 (17.3 %)
10077 (82.7 %)
Grand chelem
80 ( 7.4 %)
999 (92.6 %)
1589 (35.4 %)
2905 (64.6 %)
Vulnérabilité
NV / NV
5671 (19.3 %)
23722 (80.7 %)
6783 (23.1 %)
22610 (76.9 %)
V / NV
4122 (16.1 %)
21494 (83.9 %)
988 ( 4.9 %)
18996 (95.1 %)
NV / V
7323 (22.7 %)
24985 (77.3 %)
9821 (25.9 %)
28119 (74.1 %)
V / V
5222 (18.1 %)
23563 (81.9 %)
3136 (10.9 %)
| 25649 (89.1 %)
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
Toutefois, le comportement du joueur humain et celui du double mort sont très différents selon le type de contrat, ainsi que le révèle le tableau de droite. Pour les partielles, le double mort sait quand un contrat chute, et celui-ci est systématiquement contré. Tel n'est pas le cas pour les joueurs humains, car ils encourent de lourdes pénalités s'ils contrent des contrats qui finalement se réalisent, et ces pénalités sont beaucoup plus lourdes pour les partielles que pour les autres types de contrats. De ce fait, les joueurs humains, craignant peu d'être contrés (cf tableau 2), s'envolent en défense jusqu'à la limite supérieure de la partielle juste au-dessous de la manche. Rappelons que nous nous intéressons ici à des tournois de duplicates notés en IMPs, le comportement des joueurs humains est loin d'être semblable dans les tournois par paires notés en pourcentages du champ.
Pour les contrats de manches ou supérieurs, les joueurs humains craignent davantage le contre, et ne déclarent pas tous les contrats sous-optimaux comme le fait le double mort. Ceci est particulièrement vrai pour les chelems, car il y a en outre une forte incertitude sur la possibilité du joueur légitime de réaliser son contrat.
La vulnérabilité a évidemment une grande importance dans la décision de défendre. C'est Non Vulnérable contre Vulnérable (NV/V) que les camps sont le plus agressifs et V/NV qu'ils le sont le moins. L'agressivité du double mort dépend beaucoup plus de la vulnérabilité que celle du joueur humain : les contrats qui chutent sont systématiquement contrés, alors que les contrats de défense des humains qui chutent ne sont contrés que dans 30 % des cas (voir ci-dessous).
Répartition des contractants humains légitimes et en défense :
analyse de la réussite des contrats
CaractéristiquesContrats joués en défenseContrats joués par le camp légitime
niveau ≤ Par
niveau > Par
niveau ≤ Par
niveau > Par
Non contrés
12757
(34.5 %)
4359
(11.8 %)
67693
(84.8 %)
22759
(46.3 %)
Contrés
3657
(10.1 %)
1565
( 3.3 %)
1714
(66.2 %)
1598
(16.7 %)
| | | | | | | | | | | | | | | | | |
Dans chaque case de ce tableau apparaît, outre le nombre de contrats concernés, un pourcentage en italique qui indique le taux de succès des contrats de la case concernée. Aussi bien en défense que pour les contrats joués par le camp légitime, on distingue ceux joués à un niveau inférieur ou égal au niveau du contrat de Par, de ceux joués au-dessus du niveau du contrat de Par (ce qui peut témoigner d'une tentative de manche ou de chelem malheureuse du camp légitime ou bien d'une compétitivité exagérée). On voit ici que la défense est souvent récompensée en ce sens que son contrat n'est pas contré, même lorqu'elle dépasse le niveau du Par et que son contrat a très peu de chances de réussite.
Evidemment, il arrive que le camp légitime dépasse le niveau du Par, tout comme il arrive aussi que les opposants contrent des contrats légitimes qui ne dépassent pas le Par.
Contrats à SA : succès en fonction des points H et L
Les tableaux qui suivent présupposent que les niveaux de contrats doivent être déclarés lorsque les contrats ont une certaine probabilité de réussite. Le calcul suit la logique suivante : un déclarant demande une manche à SA (ou un petit chelem, ou un grand chelem) si le gain probable est positif. Ce gain est obtenu par la formule :
g = s p + s'(1-p)
où p est la probabilité minimum de réaliser le niveau de contrat envisagé, s est le score (en IMPs) récolté en cas de gain et s' est le score (négatif) (en IMPs) en cas de chute d'une levée.
Par exemple, si le contrat envisagé est 3SA en contexte non vulnérable, et le contrat de niveau inférieur à comparer est 1SA + 2 (2 surlevées), la marque de 3 SA étant de 400 et la marque de 1 SA + 2 étant de 150, la différence est de 250, ce qui correspond d'après le barème international à s = +6 IMPs. Si par contre, le contrat de 3 SA chute de 1 levée, la marque est de -50, alors que le contrat de 1SA+1 aurait rapporté +120, d'où une marque négative de -150-50=-200, soit s' = -5 IMPs. L'application de la formule donne:
0 < 6 p - 5 (1-p) ⇒ p > 0,455 (45,5 %)
Calcul des probabilités de succès minimum pour les contrats de manche et de petit et grand chelem
Marques et scores concernés
Manche (3SA)
Petit chelem (6SA)
Grand chelem (7SA)
Non vulnérable
Vulnérable
Non vulnérable
Vulnérable
Non vulnérable
Vulnérable
Marque en cas de succès
400
600
990
1440
1520
2220
Marque en cas de chute
-50
-100
-50
-100
-50
-100
Marque obtenue sans risque
en cas de succès
150
150
490
690
1020
1470
Score comparatif (IMPs) en cas de succès: s
6
10
11
13
11
13
Score comparatif (IMPs) en cas de chute: s'
-5
-6
-10
-12
-14
-13
Seuil de probabilité pour tenter le niveau supérieur: p
45,5 %
37,5 %
47,6 %
48 %
56 %
50 %
Seuil de probabilité moyen: p
41,5 %
47,8 %
| 53 %
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
Le tableau suivant donne, pour les donnes jouée à SA en championnat par des joueurs réels, agrégées par points d'honneur (H) et de longueur (L), le taux de succès des différents niveaux de contrats. Plus précisément, chaque case contient:
- Le nombre de donnes de la base correspondant aux caractéristiques voulues (points H et L additionnés entre le déclarant et le mort),
- En gras : le nombre moyen de levées réalisé par le déclarant,
- En italiques : Le pourcentage moyen de succès de 3 types de contrats: 3SA, 6SA et 7SA.
Les points H comme sont définis comme habituellement (As=4, Roi=3, Dame=2, Valet=1). Les points L sont donnés pour les couleurs de plus de 4 cartes, à raison de 1 par carte au-dela de la 4ème.
Le tableau n'est rempli que dans les intervalles 15 ≤ H ≤ 36 et 0 ≤ L ≤ 4, et les cases avec un échantillon de moins de 5 donnes ne sont pas représentées. Les cases sur fond coloré correspondent à une probabilité "raisonnable" de succès des contrats :
- En vert: Pour les contrats de 1SA, une probabilité d'au moins 35% de succès,
- En jaune: Pour les contrats de 3SA, une probabilité d'au moins 41,5% de succès,
- En bleu: Pour les contrats de 6SA, une probabilité d'au moins 47,8% de succès,
- En rouge: Pour les contrats de 7SA, une probabilité d'au moins 53% de succès.
Pourcentage de succès des contrats à Sans Atout en fonction de H = H1 + H2 et de L = L1 + L2
Points HPoints L
0
1
2
3
4
15
22 4.5 4.5 %/ 0.0 %/ 0.0 %
| | | | | 16
20 4.5 0.0 %/ 0.0 %/ 0.0 %
31 4.8 3.2 %/ 0.0 %/ 0.0 %
13 4.6 0.0 %/ 0.0 %/ 0.0 %
| | | 17
64 5.0 0.0 %/ 0.0 %/ 0.0 %
58 5.2 1.7 %/ 0.0 %/ 0.0 %
31 5.0 0.0 %/ 0.0 %/ 0.0 %
10 5.7 0.0 %/ 0.0 %/ 0.0 %
| | 18
160 5.4 0.0 %/ 0.0 %/ 0.0 %
160 5.8 1.2 %/ 0.0 %/ 0.0 %
89 6.1 1.1 %/ 0.0 %/ 0.0 %
12 5.9 0.0 %/ 0.0 %/ 0.0 %
| | 19
294 6.0 1.0 %/ 0.0 %/ 0.0 %
238 6.2 2.5 %/ 0.0 %/ 0.0 %
131 6.0 4.6 %/ 0.0 %/ 0.0 %
64 6.6 12.5 %/ 0.0 %/ 0.0 %
22 6.9 18.2 %/ 0.0 %/ 0.0 %
20
475 6.3 3.2 %/ 0.0 %/ 0.0 %
475 6.6 5.5 %/ 0.0 %/ 0.0 %
221 6.7 10.9 %/ 0.0 %/ 0.0 %
96 7.2 17.7 %/ 0.0 %/ 0.0 %
29 7.3 24.1 %/ 0.0 %/ 0.0 %
21
625 7.0 8.8 %/ 0.0 %/ 0.0 %
715 7.2 13.7 %/ 0.0 %/ 0.0 %
419 7.3 19.6 %/ 0.0 %/ 0.0 %
236 7.5 30.1 %/ 0.8 %/ 0.4 %
68 7.5 26.5 %/ 1.5 %/ 0.0 %
22
802 7.3 16.7 %/ 0.0 %/ 0.0 %
1103 7.5 22.9 %/ 0.0 %/ 0.0 %
663 7.8 32.6 %/ 0.5 %/ 0.0 %
335 8.0 43.0 %/ 2.1 %/ 1.2 %
107 8.1 45.8 %/ 0.0 %/ 0.0 %
23
844 7.8 23.7 %/ 0.0 %/ 0.0 %
1330 8.0 33.8 %/ 0.3 %/ 0.0 %
969 8.3 42.2 %/ 0.5 %/ 0.1 %
494 8.3 46.2 %/ 2.0 %/ 0.2 %
166 8.2 48.2 %/ 0.6 %/ 0.6 %
24
980 8.2 36.7 %/ 0.1 %/ 0.1 %
1451 8.4 48.4 %/ 0.2 %/ 0.0 %
1155 8.6 57.0 %/ 0.6 %/ 0.1 %
636 8.8 61.9 %/ 3.3 %/ 0.5 %
158 8.6 53.2 %/ 4.4 %/ 0.0 %
25
921 8.6 60.0 %/ 0.1 %/ 0.0 %
1588 8.8 63.8 %/ 0.5 %/ 0.0 %
1163 9.1 69.8 %/ 1.7 %/ 0.1 %
729 9.4 74.3 %/ 9.1 %/ 1.0 %
171 9.0 62.6 %/ 4.7 %/ 1.8 %
26
840 8.9 68.0 %/ 0.1 %/ 0.0 %
1404 9.3 79.0 %/ 2.3 %/ 0.1 %
985 9.5 78.4 %/ 5.8 %/ 0.4 %
448 9.7 79.5 %/13.4 %/ 1.3 %
179 9.7 82.7 %/11.7 %/ 3.9 %
27
600 9.4 84.0 %/ 2.0 %/ 0.0 %
986 9.8 87.7 %/ 6.2 %/ 0.6 %
685 10.0 89.3 %/12.1 %/ 1.5 %
388 10.2 89.4 %/19.1 %/ 4.4 %
100 10.4 85.0 %/31.0 %/ 8.0 %
28
404 10.0 93.1 %/ 2.5 %/ 0.0 %
675 10.3 92.7 %/14.2 %/ 1.9 %
540 10.4 94.1 %/21.7 %/ 2.4 %
283 10.7 94.7 %/31.1 %/ 6.7 %
63 10.4 93.7 %/22.2 %/ 3.2 %
29
322 10.2 96.0 %/ 7.5 %/ 0.0 %
631 10.5 97.3 %/16.6 %/ 2.4 %
383 10.8 96.3 %/29.2 %/ 4.2 %
139 10.9 95.0 %/35.3 %/ 7.9 %
36 10.5 83.3 %/44.4 %/13.9 %
30
234 10.7 99.6 %/15.4 %/ 0.9 %
293 11.1 100.0 %/33.4 %/ 3.4 %
161 11.4 100.0 %/51.6 %/ 6.8 %
138 11.4 98.6 %/52.9 %/23.2 %
32 11.2 96.9 %/43.8 %/15.6 %
31
201 11.0 98.5 %/28.4 %/ 2.0 %
182 11.3 98.4 %/45.6 %/ 4.4 %
110 11.6 100.0 %/60.0 %/ 6.4 %
44 11.5 93.2 %/65.9 %/15.9 %
20 12.2 100.0 %/85.0 %/45.0 %
32
66 11.4 100.0 %/54.5 %/ 4.5 %
103 11.6 100.0 %/57.3 %/20.4 %
69 12.1 100.0 %/84.1 %/26.1 %
34 12.2 100.0 %/94.1 %/29.4 %
14 12.5 100.0 %/100.0 %/50.0 %
33
33 11.7 100.0 %/66.7 %/ 6.1 %
47 12.2 100.0 %/93.6 %/23.4 %
29 12.5 100.0 %/96.6 %/51.7 %
43 11.9 97.7 %/74.4 %/32.6 %
| 11 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |


